بحث عن الاتصال والنهايات

علم التفاضل والتكامل هو أحد أهم فروع الرياضيات الذي يعنى بحساب معدلات التغير الكمية. يعد هذا العلم أساسيًا في فهم العديد من المبادئ والتطبيقات في مجالات مختلفة مثل الفيزياء والهندسة وعلوم الحاسوب. وفي هذا السياق، نقدم لكم بحثًا مفصلاً عن الاتصال والنهايات الممثلة لبدايات علم التفاضل والتكامل. سيتم تناول الموضوع بشكل مفصل وشامل على موقعنا، حيث سيتم طرح المفاهيم الأساسية والأدوات الرياضية المستخدمة في هذا العلم.

سيستفيد القراء من شرح واضح ومبسط للمفاهيم الصعبة، مع توضيح العلاقة بين التفاضل والتكامل وتطبيقاتهما في الحياة العملية. ستقدم في النهاية نصائح للتعلم الفعال لهذا العلم الشيق والمهم. نتمنى لكم قراءة ممتعة ومفيدة.
تعد النهايات أدوات مهمة جدًا في فرع التفاضل والتكامل الرياضي، في أغلب الأحيان تكون بناء أولي يبنى عليه عمليات حسابية أشد تعقيدًا.
مقدمة البحث
النهايات تعتبر من أهم المبادئ الرياضية المختصة بعلم التفاضل.. حيث يهتم العلم بدراسة الاشتقاق، وذلك عن طريق الدراسة العميقة في الكميات المتناهية في الصغر وتقسيمها.
تم بناء الاشتقاق على النهايات لدراسة الاشتقاق الدالي؛ على هذا فإن كل من مفهوم النهايات ومفهوم الاشتقاق مرتبطان بصورة وثيقة بكافة التغيرات التي تحدث للدالة.
لأهمية الموضوع هذا نقدم لكم بحث عن الاتصال والنهايات متواضع نرجو أن ينال إعجاب حضراتكم
عناصر البحث
سنتناول في هذا البحث عن الاتصال والنهايات عدة عناصر هي:
- تعريف النهايات.
- تعريف النهاية رياضيًا.
- خواص النهايات.
- الاتصال عند نقطة.
- متى تكون الدالة متصلة.
- اتصال الدوال.
- الاتصال على فترة.
- نظريات الدوال.
- النهايات في التاريخ.
- أهمية الاتصال والنهايات.
تعريف النهاية
حينما تقترب قيمة س من قيمة معينة فإن القيمة التي تقترب منها الدالة كثيرًا تلك هي النهاية.
تعريف النهاية رياضيًا
تكون صورة ترميز النهاية كالتالي:
نها د (س)= ل
هذه الصورة تكون صحيحة بشرط أن تكون القيمة الكلية لـ د(س) قريبة من ل وتقترب س من أ دون أن تساويها
يمكن التوضيح بالصورة الآتية:
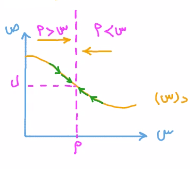
قد نص التعريف الذي ذكرناه سابقًا أنه عندم تكون (س) قريبة من (ل) فتخبرنا النهاية أن قيمة د(س) تقترب من قيمة (ل) كلما اقتربت (س) من (أ)
كما ذكرنا في التعريف أن هذه العلاقة تتم في الجهتين فهذا يدل على أنه قد يحدث في:
- الاتجاه الموجب عندما تكون قيمة (س) أكبر من قيمة (أ) في الاتجاه للقيم الموجبة
- الاتجاه السالب عندما تكون قيمة (س) أقل من قيمة (أ) في الاتجاه للقيم السالبة.
القراء الذين اضطلعوا على هذا الموضوع قد شاهدوا أيضًا..
خواص النهايات
هناك عدد من خواص النهايات مثل نهايات الجمع ونهايات الطرح وحاصل ضرب نهايتين وأيضًا نهايات خارج القسمة دالتين، وعلى افتراض أن:
د (س)، ق (س) دالتان وحيث (أ) قيمة ما، ونها د (س) ونها (س) موجودتان فنكتشف أن:
- نهايات مجموع أكثر من دالة
نها (د (س) + ق (س)) = نها د (س) + نها ق (س)
- نهايات الفرق بين دالتين
نها (د (س) – ق (س)) = نها د (س) – نها ق (س)
يمكن تطبيق هاتان الخاصيتان معًا على النهاية التي نحاول إجادها.
هكذا تعرفنا على أول خاصيتين لنهايات الدوال ولكي نتعرف على باقي خواص نفترض أن:
لدينا د (س)، ق (س)، وقسيمتين ثابتتين هما (أ) و(ج)، مع أن نها د (س) ونها ق (س) موجودتان، فنكتشف أن:
- الثوابت المضروبة داخل النهاية
نها جـ × د (س) = جـ × نها د (س)
هذه الخصية تدل على أنه إذا كان هناك عامل مشترك داخل نهاية يمكن بسهولة إخراجه خارج النهايات.
- حاصل ضرب دالتين
نها (د (س) × ق (س)) = نها د (س) × نها ق (س).
- نهاية خارج قسمة الدوال
نها د (س)/ ق (س) = نها د (س)/ نها ق (س).
يجب أن نعرف أن كل خاصية من هذه الخواص يمكن أن نستخدمها مع غيرها من الخواص الأخرى (بما فيهم نهاية مجموع أكثر من دالة ونهاية الفرق بين دالتين).
الاتصال عند نقطة
فهم الاتصال عند نقطة يعتبر مهم جدًا لفهم ما يترتب عليه من دوال المتصلة.
أنواع الدوال المتصلة:
- الدوال كثيرة الحدود.
- الدوال الأسية.
- المثلثية المحددة (بعضها).
- الدوال الكسرية.
ويمكن جمها تحت حكم (الدوال التي يمكن تمثيلها بيانيًا بخط واحد)
متى تكون الدالة متصلة
لتكون الدالة د متصلة عند النقطة (أ) إذا كان نها د (س) = د (أ) عندما يقترب س من أ.
بذلك نكون وصلنا إلى التعريف الرياضي للاتصال عند نقطة.
شروط أن تكون الدالة متصلة عند نقطة.
هناك عدة شروط لكي تكون المعادلة السابقة متحققة وتكون الدالة متصلة، مثل:
- أن يكون الطرف الأيمن من المعادلة متحقق، أي أن هذه النهاية موجودة، نها (س) موجودة عندما تقارب س إلى أ.
- يجب أن يتم تعريف د عند أ، فإذا لم يكن هكذا فالطرف الأيسر من المعادلة غير معرف والنهاية ليست متصلة بسبب عدم تحقيق المعادلة
- (د) معرفة عند (أ) أي أن (أ) تقع ضمن المجال الخطي لـ (د).
- يمكن أن يكون شق المعادلة الأيمن موجود والشق الأيسر معرف ولكن النهاية غير متصلة بسبب أن القيمتان ليستا متساويتان، لذلك يجب التساوي بين شقي المعادلة حتى تكون الدالة متصلة.
اتصال الدوال
تكون الدالة متصلة عند نقطة إذا تحقق التعريف العام الآتي:
الدالة د (س) متصلة عند النقطة س = أ على اعتبار:
- نها د (س) عندما تقترب س من أ = د (أ)
بالطبع يجب أن تكون هتان القيمتان موجوداتنا وهذا يتطلب بالتبعية تحقيق نها د (س) عندما تقترب س من أ- = نها د (س) عندما تقترب س من أ– = ل
ويجب أن تكون د (أ) = (ل)
الاتصال على فترة
هناك تعريف دارج للاتصال على فترة يقول: “الاتصال على فترة هي الدالة التي تستطيع رسم التمثيل البياني لها دون أن ترفع القلم عن الورقة”.
أما الطريقة الدقيقة لهذا التعريف تقول:
“أن الدالة د (س) متصلة على فترة إذا كان شرط الاتصال عند النقاط على كل قيم (س) قد تحقق ضمن تلك الفترة”
أهم طرق التحقق من الاتصال على فترة هي بالتأكد من عدم وجود نقاط عدم اتصال على في الفترة المذكورة.
الرسم البياني للدوال الغير متصلة يكون مثل:
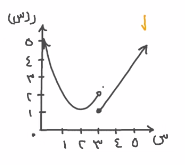
الرسم البياني للدالة المتصلة يكون مثل:
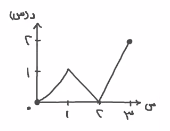
نظريات الدوال
هناك ثلاث نظريات للدوال هي:
نظرية اتصال الدوال
الدالة المتصلة هي التي يمكن رسمها بخط بياني واحد مستوي.
نظرية عدم اتصال الدوال
تكون الدالة غير متصلة إذا تم تمثيلها بيانيًا عن طريق خطين لا خط واحد واتصال قفزي أو اتصال يقبل إزالته.
أنواع عدم الاتصال
هناك ثلاث أنواع لعدم الاتصال هم:
عدم اتصال لا نهائي.
عدم اتصال قابل للإذالة.
القيمة المتوسطة.
عدم اتصال قفزي.
تنص القيمة المتوسطة على أنه عند اتصال الدوال من نقطة ما إلى أي نقطة أخرى فإن أي قيمة واقعة بين النقطتين تقوم الدالة بتحقيقها.
النهايات في التاريخ
نشأ مفهوم النهايات في بدئ الأمر بسبب الحاجة المتزايدة إلى طريقة لحساب الأطوال والمساحات والأحجام (مثل مساحة الدائرة وحجم الكرة)، وتم ذلك عن طريق تطوير مفهوم الاستنفار القديم الذي استخدمه اليونانيون وبه قام أرخميدس بحساب مساحة الدوائر.
أهمية الاتصال والنهايات
تقبع الأهمية العملية للاتصال والنهايات أنه يرتبط ارتباطًا وثيقًا بعلم الفيزياء وعلم الميكانيكا، وبه تتم عمليات حسابة كانت مستحيلة دونه.
خاتمة البحث
هكذا نكون قد قدمنا لكم بحثنا المتواضع حول موضوع دراستنا في الاتصال والنهايات نرجو أن يكون قد نال إعجابكم، وقد تحرينا الدقة فيما أوردنا بمساعدة أساتذتنا الكرام.
بذلك نكون قد قدمنا لكم نموذج بحث عن الاتصال والنهايات جاهز للطباعة مفسر فيه المقدمة والعناصر والموضوع والخاتمة، نرجو أن نكون قد أفدناكم.
