حساب مساحة شبه المنحرف شرح موضح بالأمثلة
هناك طريقتين مختلفتين يمكنك حساب مساحة شبه المنحرف من خلالهما، وتلك الطرق تُستخدم في جميع أشكال شبه المنحرف سواءً كان شبه المنحرف القائم أو المتساوي الساقين أو الغير المنتظم، لذلك ومن خلال الموضوع التالي المقدم لكم من خلال موقع مثقف سنعرض حساب مساحة شبه المنحرف.
حساب مساحة شبه المنحرف
الشبه المنحرف هو واحد من الأشكال الرباعية والتي يتقابل فيها ضلعان متوازيان بأطوال مختلفة وهم قاعدتي شبه المنحرف، والضلع الأكبر فيهما يمثل القاعدة الكبرى، والضلع الأصغر فيهما يمثل القاعدة الصغرى، وهناك ضلعان آخران وهم الساقين.
هناك عدة طرق يمكن من خلالها الوصول لمساحة شبه المنحرف، وهذه الطرق هي:
- مساحة شبه المنحرف= (مجموع طول القاعدتين) /2 X الارتفاع، والارتفاع هو ضلع عمودي وقائم الزاوية على القاعدة الكبرى، (مجموع طول القاعدتين مقسوم على 2 والناتج يتم ضربه في الارتفاع)
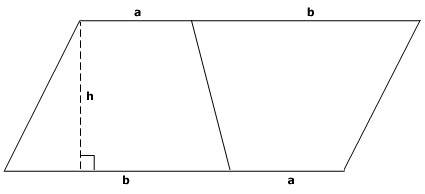
- يمكن حساب المساحة من خلال تقسيم شبه المنحرف إلى أشكال مثل مربع ومثلث أو مستطيل ومثلث أو متوازي الأضلاع ومثلث؛ بهدف توفير أشكال هندسية يسهل حساب مساحتها ومن ثم يتم جمع مساحة تلك الأشكال معًا للوصول لمساحة شبه المنحرف.
إذا قمنا مثلًا بتقسيم شبه المنحرف إلى مستطيل ومثلثين يتم الوصول لمساحة شبه المنحرف من خلال جمع مساحة المثلث الأول مع مساحة المثلث الثاني مع مساحة المستطيل.
أمثلة حساب مساحة شبه المنحرف
- مثال: إذا كان هناك شبه منحرف طول أحدى القاعدتين 5 سم والقاعدة الأخرى 10 سم، ويكون ارتفاع شبه المنحرف 7 سم، قم بحساب المساحة.
الحل:
مساحة شبه المنحرف= (مجموع طول القاعدتين) /2 X الارتفاع
مساحة شبه المنحرف= (5+10) /2 X 7= 52.5 سم2
- مثال: إذا كان هناك شبه منحرف ومجموع طول القاعدتين فيه هو 40 سم، والارتفاع يساوي 18 سم، قم بحساب مساحة شبه المنحرف.
الحل:
يتم الوصول لمساحة شبه المنحرف من خلال القانون 1/2 X (مجموع القاعدتين) X الارتفاع.
إذًا مساحة شبه المنحرف= 1/2X (40) X 18
مساحة شبه المنحرف= 18 X 20= 360 سم2
- مثال: إذا كان هناك شبه منحرف فيه طول القطعة المتوسطة هو 14 وارتفاعه يساوي10سم، قم بحساب مساحة شبه المنحرف.
الحل:
في حالة معرفة طول القطعة الواصلة بين جانبي شبه المنحرف، إذًا فإن مساحة شبه المنحرف تساوي طول القطعة المتوسطة X الارتفاع.
إذًا مساحة شبه المنحرف= 14 X 10= 140 سم2.
في حالة حساب مساحة شبه المنحرف من خلال الطريقة الثانية بتقسيمه إلى أشكال هندسية مختلفة حتى يسهُل على الطالب حساب مساحته نقوم بالتالي:
مثال: إذا كان هناك شبه منحرف طول قاعدته الصغرى تبلغ 3 سم، ومقسم إلى 3 أشكال مثلثين ومستطيل، ويكون ارتفاع شبه المنحرف 4 سم، وطول ضلع المثلث الأول 2 سم، وطول ضلع المثلث الثاني 2 سم، قم بحساب مساحة شبه المنحرف.
الحل:
- مساحة المثلث= (طول القاعدة X الارتفاع) /2
- إذًا فمساحة المثلث الأول= (2X 4) /2= 4سم2
- مساحة المثلث الثاني= (1 X 4) /2= 2سم2
- مساحة المستطيل= الطول X العرض
- إذًا مساحة المستطيل= 3 X4 =12سم2
- وبذلك مساحة شبه المنحرف= مساحة المثلث الأول+ مساحة المثلث الثاني+ مساحة المستطيل
- مساحة شبه المنحرف= 4+ 2+ 12= 18سم2
القراء الذين اضطلعوا على هذا الموضوع قد شاهدوا أيضًا..
أنواع شبه المنحرف
هناك العديد من الأنواع المختلفة لشبه المنحرف، فهناك شبه منحرف عام، وشبه منحرف مختلف الأضلاع، وشبه منحرف قائم الزاوية، وشبه المنحرف متساوي الساقين، سنعرض تلك الأنواع فيما يلي بالتفصيل.
شبه المنحرف العام
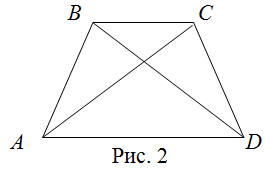
شبه المنحرف العام هو مضلع رباعي، ويتكون من ضلعان متوازيان، قطران يتقابلان في نقطة ما وغير متساويان، ويكون الارتفاع في شبه المنحرف العام هو المسافة العمودية بين الضلعين المتوازيين.
يضم هذا النوع من شبه المنحرف 4 زوايا غير متساوية ويكون مجموعهم 360 درجة، ويكون فيه كل زاويتين محصورتين بين الضلعين المتوازيين ويكون مجموعهما 180 درجة.
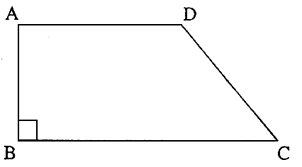
شبه المنحرف القائم
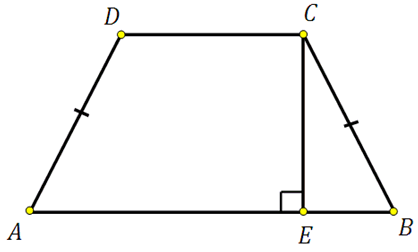
يكون شبه المنحرف القائم عبارة عن مضلع رباعي يضم زاويتين قائمتين، ويكون ارتفاع شبه المنحرف القائم متمثل في الضلع العمودي على القاعدة الكبرى.
شبه المنحرف متساوي الساقين
يكون شبه المنحرف متساوي الساقين عبارة عن مضلع رباعي يضم ضلعين متوازيين ومتقابلين، ويكون فيه زاويتي قاعدتيه متطابقتين، والضلعين الآخرين غير متوازيين ولكن متساويين في الطول ومتقابلين.
شبه المنحرف غير منتظم
يكون شبه المنحرف الغير منتظم في أضلاعه عبارة عن مضلع رباعي يضم ضلعان يكونان قاعدتيه وهم متوازيان غير متساوين، ويضم قطران يتقاطعان في نقطة ما وغير متساويين، ويضم ضلعان غير متساويين وغير متوازيين.
تكون مجموع زوايا شبه المنحرف الغير منتظم هي 360 درجة.
مساحة شبه المنحرف القائم الزاوية
في شبه المنحرف القائم يكون هناك إحدى الساقين عمودية على القاعدتين، وفي هذه الحالة يتم اعتبار طول الساق هو الارتفاع، وفي تلك الحالة يكون مساحة شبه المنحرف القائم= 1/2 X (مجموع القاعدتين) X طول الساق العمودي.
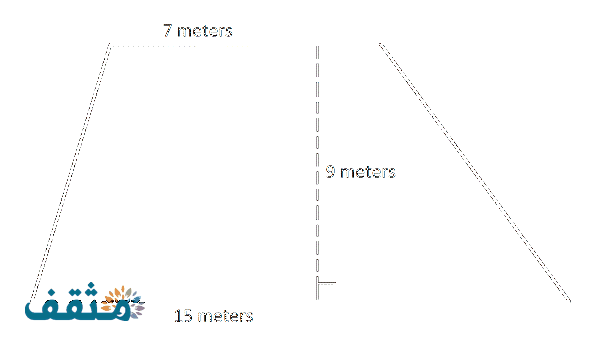
مثال: إذا كان هناك شبه منحرف فيه طول إحدى القاعدتين 9سم، والقاعدة الأخرى 5سم، وطول الساق العمودي 7سم، قم بحساب مساحة شبه المنحرف.
مساحة شبه المنحرف= 1/2 X (مجموع القاعدتين) X طول الساق.
مساحة شبه المنحرف= 1/2 X (5+9)X 7= 49 سم2.
مساحة شبه المنحرف غير المنتظم
غالبًا ما يصاحب شبه المنحرف الغير منتظم ذكر لأطوال قاعدتيه وساقيه فقط وعليك أن تأتي بالارتفاع بنفسك حتى تتمكن من الوصول إلى حساب مساحته، إليك بعض الأمثلة.
- مثال: إذا كان هناك شبه منحرف طول قاعدته الصغرى 16سم، وطول قاعدته الكبرى 25سم، وطول أحد سيقانه 12سم، والزاوية بين الساق والقاعدة هي 30 درجة، قم بحساب مساحة شبه المنحرف.
الحل:
في حالة معرفة قيمة الزاوية وقيم طول الضلع يمكنك استخدام قانون فيثاغورس أو قاعدة الجيب وجيب التمام حتى تتمكن من معرفة الارتفاع والذي يمكنك الوصول إلى المساحة من خلاله.
يمكنك الوصول إلى الارتفاع من خلال قانون جيب الزاوية وهو جا (الزاوية)= الارتفاع/ الوتر.
جا 30= الارتفاع/ 12سم، إذًا فالارتفاع= 6سم.
بعد الوصول إلى الارتفاع يمكنك بسهولة الوصول لمساحة شبه المنحرف من خلال القانون الخاص به وهو 1/2X (مجموع طول القاعدتين)X الارتفاع.
إذًا مساحة شبه المنحرف الغير منتظم= 1/2 X (16+25) X 6= 123سم2.
طريقة الوصول لقانون مساحة شبه المنحرف
القانون الثابت لمساحة شبه المنحرف هو 1/2 X (مجموع القاعدتين) X الارتفاع، وتم استنتاج هذا القانون رياضيًا عن طريق:
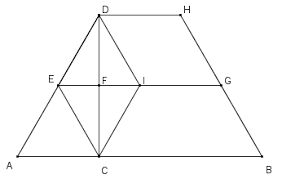
- تم تقسيم شبه المنحرف إلى 3 أشكال هندسية وهم مثلثين ومستطيل وأصبحت مساحة شبه المنحرف تساوي مساحة المثلث الأول+ مساحة المثلث الثاني+ مساحة المستطيل.
بذلك أصبح مساحة شبه المنحرف= (1/2) قاعدة المثلث الأول X ارتفاعه+ )1/2) Xقاعدة المثلث الثاني X ارتفاعه + طول المستطيل X عرضه، وذلك يمكن أن يُوضح من خلال بعض الرموز.
نفترض أنه تم تقسيم شبه المنحرف إلى مثلث أول قائم طول قاعدته هي “هـ”، ويكون ارتفاعه هو “ع”، ومثلث آخر قائم تكون قاعدته “ن” وارتفاعه “ع”، والمستطيل قاعدته “ل” وارتفاعه “ع”، وبذلك مساحة المثلث الأول تساوي (1/2)X هـX ع، ومساحة المثلث الثاني تساوي (1/2)X نX ع، وتكون مساحة المستطيل تساوي لXع.
نتيجة لذلك فإن مساحة شبه المنحرف= (1/2) Xهـ Xع+ (1/2)Xن Xع+ لx ع، وبضرب الطرفين X2 يصبح 2X مساحة شبه المنحرف= هـX ع+ لXع+ 2ل Xع، ومع أخذ “ع” عامل مشترك يصبح 2X مساحة شبه المنحرف= عX (هـ+ن+2ل).
من ثم نقوم بالقسمة على 2، وبمعرفة أن (هـ+ ن+ ل) تساوي طول القطعة السفلية وهو 2، وأن “ل” هو طول القاعدة العلوية، يكون مساحة شبه المنحرف= 1/2X (ل+ل2) Xع.
هكذا نكون قد عرضنا لكم من خلال الموضوع السابق حساب مساحة شبه المنحرف والذي يتضمن حساب مساحة لأنواع شبه المنحرف المختلفة، وعرضنا لكم أيضًا طريقة الوصول إلى القانون العام الخاص بمساحة شبه المنحرف.