مساحة شبه المنحرف
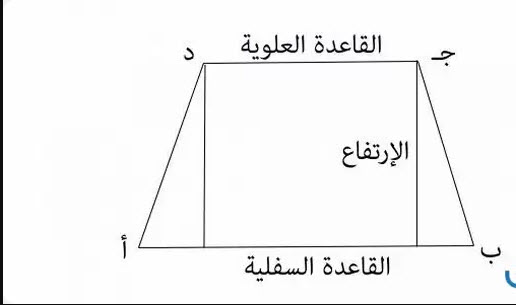
مساحة شبه المنحرف، تُحسب من خلال طرق متعددة، والطرق المستخدمة طبقًا لما جاء في نظريات علماء الرياضيات، وتحديدًا عند المتخصصين في الهندسة الفيزياء، ويُعد شبه المنحرف من الأشكال الهامة في مجال الهندسة، وهو عبارة عن أضلاع رباعية كل ضلعين فيه متوازيان مثله مثل المربع والمستطيل، ويختلف عنهما في عدم تساوي أطوال أضلاع، واحتوائه على قاعدتين الكبرى وهي أكبر الأضلاع طولًا، والصغرى التي تُعد أصغر الأضلاع طولًا.
مساحة شبه المنحرف
توجد عدة معادلات رياضية وطرق لحساب المساحة، وهي كالآتي:
(طول القاعدة الكبرى + طول القاعدة الصغرى ÷ 2 ) × الارتفاع.
يجب الإشارة إلى أن شبه المنحرف يقسم إلى أشكال أخرى، وهي كالتالي:
- مستطيل والمثلث أو المربع بالإضافة إلى مثلث.
- متوازي أضلاع مثلث.
- مثلثين ومستطيل.
- في حالة تقسيم شبه المنحرف إلى مثلثين ومستطيل، يتم حساب مساحته بالطريقة الآتية: (مجموع مساحة المثلثين + مساحة المستطيل).
هذا يعني أننا سنحصل على مساحة المثلث من خلال:
- (ضرب طول القاعدة × الارتفاع) ثم نقسم الناتج على 2.
- (ضرب نصف طول القاعدة × الارتفاع) ثم نقسمهم على 2.
- نجمع طول ضلعي الزاوية القائمة ثم نقسمهم على 2.
- يتم احتساب مساحة المستطيل بعد احتساب مساحة كل مثلث على حدى، ثم جمع نتيجة المساحتين، وذلك من خلال ضرب طول المستطيل في عرضه.
مساحة شبه المنحرف بطرق أخرى
يُمكن حساب المساحة عن طريق استعمال طرق أخرى، ويمكن ذكر بعضها في النقاط التالية كالآتي:
- ( نصف طول القاعدة الأولي + طول القاعدة الثانية ) × الارتفاع.
- حساب مساحة شبه المنحرف من خلال صيغة هيرون وهي، م = ( ( و- أ ) ( و – ب ) ( و – أ – ج ) ( و – أ – د ) ) √ × ( أ + ب ) / ( أ – ب ).
يُذكر أن الحروف المذكورة في قانون هيرون ترمز إلى ما يلي:-
- م: ويعني مساحة شبه المنحرف.
- أ: معناه طول القاعدة السفلية.
- ب: يرمز إلى طول القاعدة العلوية.
- ج، د: معناهما طول الساقين.
- و: وهو نصف محيط شبه المنحرف.
- يتم احتسابه من خلال جمع (طول القاعدة السفلية + طول القاعدة العلوية + طول الساقين) وقسمة الناتج على 2.
يتم احتساب المساحة الخاصة بشبه المنحرف في حالة وجود طول الخط المستقيم المتوسط، من خلال القانون الآتي:
- طول الخط المتوسط × الارتفاع.
- يقسم شبه المنحرف إلى مثلثين من خلال إسقاط عمودين من زوايا القاعدة الأولى حتى يصل للقاعدة الثانية.
- استخدام نظرية العالم فيثاغورس للمثلث منفردًا وذلك بهدف احتساب طول قاعدة المثلث من خلال القانون التالي، مربع الوتر = مربع الضلع الأول + مربع الضلع الثاني.
- يتم حساب طول القاعدة الثانية لشبه المنحرف من خلال طول القاعدة الأولى مجموع على مجموع قاعدتي المثلثين.
- تطبق معادلة مساحة شبه المنحرف وهي (نصف × مجموع طول القاعدتين الأولى والثانية × الارتفاع).
ما هي أنواع شبه المنحرف
شبه المنحرف له عدة أنواع وتختلف أنواعه على حساب قياسات أضلاعه، لأنه كما ذكرنا في البداية هو شكل رباعي الأضلاع، وتتمثل أنواع متوازي الأضلاع فيما يلي:
شبه المنحرف العام
- يحتوي على قطرين مختلفين في القياس، ومتقابلين في نقطة معينة وارتفاعه عمودي بين ضلعين متوازيين.
- يتكون من أربع زوايا ليست متساوية ويكون مجموع قياسها 360 درجة، ومجموع الزاوية المحصورة بين الضلعين المتوازيين هو 180 درجة.
النوع الثاني
- شبه منحرف يتكون من ضلعين متقابلين متوازيين، وضلعين آخرين متقابلين متساويين في الطول لكنهما غير متوازيين.
- ويُعرف بشبه المنحرف ذو الساقين المتساويين الذي يتساوى فيه طول القطرين.
شبه المنحرف المختلف في أطوال أضلاعه
- يحتوي على 4 أضلاع منهما ضلعين متوازيين، لكنهما لا يتساويان معًا في الطول.
- هذين الضلعين هما قاعدتي شبه المنحرف، كما يحتوي هذا النوع على ضلعين آخرين غير متساويين في الطول.
- قطريه لا يساوي بعضهما في الطول ولكنهما يتقاطعان في نقطة معينة.
شبه المنحرف ذو الزوايا القائمة
- يتكون من زاويتين قائمتين ويعتبر الارتفاع هو الضلع العمودي على القاعدة الكبيرة، وهذا الضلع يمثل أهمية كبيرة في أضلاع شبه المنحرف.
قوانين شبه المنحرف المهمة
محيط شبه المنحرف
يتم احتساب محيط شبه المنحرف من خلال قوانين متعددة وهي:
- محيط شبه المنحرف = مجموع أطوال أضلاعه الأربعة.
- محيط شبه المنحرف = جمع القاعدتين العلوية والسفلية مع الارتفاع × ( 1 / جا زاوية القاعدة اليمنى ) + ( 1/ جا زاوية القاعدة اليسرى ).
تُعد زاوية القاعدة الأولى هي الزاوية التي تنحصر بين القاعدة السفلية والساق الأول، أما زاوية القاعدة اليسرى فهي الزاوية التي تنحصر بين القاعدة السفلية والساق الثاني لشبه المنحرف.
شبه المنحرف قائم الزوايا
- محيطه = طول أحد أضلاع شبه المنحرف الذي يكون الزاوية القائمة مع ضلعين آخرين + طول الضلعين المتوازيين لشبه المنحرف + الجذر التربيعي لقيمة مربع طول الضلع الذي تتكون فيه الزاوية القائمة + مربع الفرق بين طول الضلعين المتوازيين لشبه المنحرف.
شبه المنحرف متساوي الساقين
- محيطه = مجموع أطوال القاعدتين العلوية والسفلية + 2 × طول الضلعين غير المتساويين في الطول.
ارتفاع شبه المنحرف
- (يساوي 2 × مساحة شبه المنحرف) / مجموع طول القاعدتين السفلية والعلوية.
أقطار شبه المنحرف
طول القطر ( هـ ي ) = الجذر التربيعي لناتج المعادلة الآتية:
- مربع أ + مربع د – 2 × ب × أ × جتا (و )، أما طول القطر ( د و ) فإنه = الجذر التربيعي ناتج المعادلة الآتية:- مربع ب + مربع جـ – 2 × ب × ج × جتا ( ي ).
ترمز حروف المعادلات إلى ما يأتي:
- ( هـ ي )، ( د و ) = قطري شبه المنحرف.
- أ، جـ = طول الضلعين غير المتوازيين في شبه المنحرف؛ يرمز الـ ( أ ) إلى الضلع الأيسر بينما يرمز ( جـ ) الضلع الأيمن.
- ب = طول القاعدة العلوية، أما د = طول القاعدة السفلية
- و = الزاوية المحصورة بين القاعدة د، والضلع أ.
- ي = الزاوية المحصورة بين القاعدة د، والضلع جـ.
- مربع ن + مربع هـ = مربع أ + مربع جـ + ( 2 × د × ب )
- يساوي ن و هـ قطري شبه المنحرف.
- يرمز أ وجـ إلى طول الضلعين الأيسر والأيمن
- يعني ب طول القاعدة العلوية أما د فهو القاعدة السفلية لشبه المنحرف.
طول الخط المتوسط لشبه المنحرف
- يعني الخط الذي يصل بين نقطة منتصف شبه المنحرف، والضلعين غير المتوازيين وهو خط متوازي مع القاعدتين السفلية والعلوية.
- يُذكر أن هذا الخط يساوي متوسط طول القاعدتين ويتم احتسابه من خلال القانون الآتي: 1/2 × ( طول القاعدة الأولي + طول القاعدة الثانية ).
وبهذا نكون قد أوضحنا بالتفصيل كيفية حساب مساحة شبه المنحرف بكافة أنواعه، وأهم القوانين المتعلقة به مثل المحيط والخط المتوسط، كما بينا أن المساحة لشبه المنحرف تحتسب بطرق متعددة، منها السهل والبسيط ومنها ما هو معقد إلى حد كبير، يُترك لأي منا حرية اختيار الطريقة الأسهل في وجهة نظره، حيث يختلف هذا الأمر من عقل بشري إلى آخر.
عزيزي القاريء نتمني أن نكون قد قدمنا كافة المعلومات لموضوع مساحة شبه المنحرف في المملكة عبر موقع محتوى ونحن على أتم الاستعداد لرد على إستفساراتكم في أسرع وقت.
